11 Quelques tests statistiques

11.1 Comparaison de proportions

11.1.1 Test du \(\chi^2\) (paramétrique)

Mesure l’écart qui existe entre l’effectif observé et l’effectif attendu. Cet écart est-il simplement lié au hasard?

11.1.1.1 Hypothèses

  • H0 : Les proportions sont identiques entre les groupes
  • H1 : Au moins un groupe diffère dans ces proportions

11.1.1.2 Fiabilité

  • \(\alpha\)=0.05 avec n>6gk
  • \(\alpha\)=0.01 avec n>10gk

avec g le nombre de groupes et k le nombre de classes

11.1.1.3 Exemple

Dans le cadre de la DCE, vous devez inventorier les plages ayant subis des marées vertes par masses d’eau.

##                    Artois Picardie Seine Normandie Loire Bretagne Adour Garonne
## Pres marees vertes               8              11             20             6
## Abs marees vertes                4              14             12             3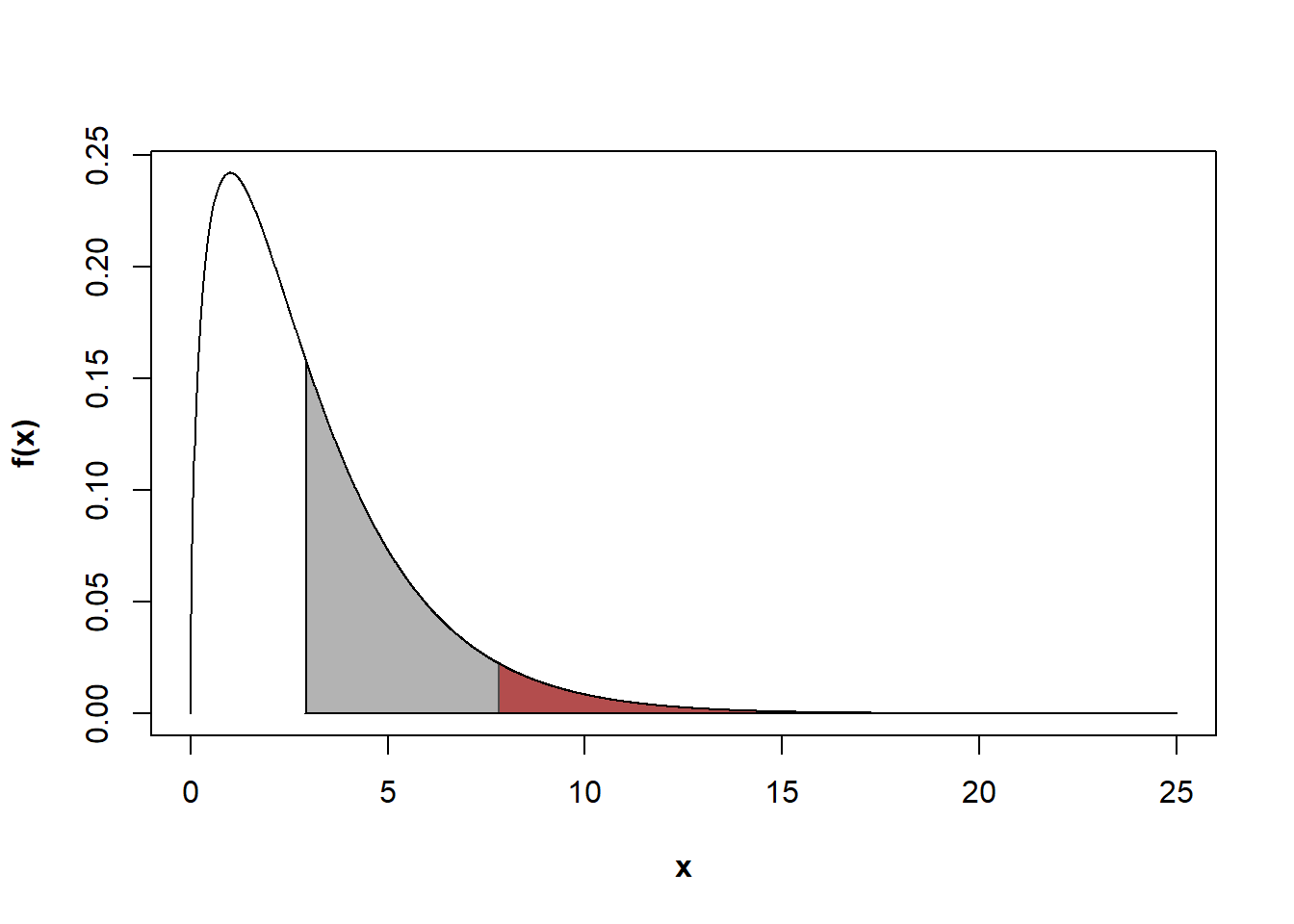
Fonction de densité associée à une loi du $\chi^2$ avec 3 ddl.

Figure 11.1: Fonction de densité associée à une loi du \(\chi^2\) avec 3 ddl. 

 bassin <- rbind(c(8,11,20,6),c(4,14,12,3))
 colnames(bassin) <- c("Artois Picardie","Seine Normandie","Loire Bretagne",
                       "Adour Garonne")
 row.names(bassin) <- c("Pres marees vertes","Abs marees vertes")
 bassin <- as.data.frame(bassin)
 chisq.test(bassin)
## 
## 	Pearson's Chi-squared test
## 
## data:  bassin
## X-squared = 2.9162, df = 3, p-value = 0.4047

11.1.2 Test exact de Fisher (non-paramétrique)

Lorsque la validité du test du \(\chi^2\) n’est pas assurée, le test exact de Fisher en est la parade.

11.1.2.1 Hypothèses

  • H0 : Les proportions sont identiques entre les groupes
  • H1 : Au moins un groupe diffère dans ces proportions

11.1.2.2 Exemple

Vous avez étudié l’expression des protéines régulant le transport des ions K+ suite à des stress thermiques de 24°C et 26°C sur un total de 20 huitres creuses.

##            T24 T26
## active       3   8
## non-active   7   2
fisher.test(stress)
## 
## 	Fisher's Exact Test for Count Data
## 
## data:  stress
## p-value = 0.06978
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.007870555 1.133635839
## sample estimates:
## odds ratio 
##  0.1226533

11.2 Une variable et 2 échantillons

11.2.1 Test t de student (paramétrique)

Comparaison de moyennes de deux distributions normales de variances inconnues mais supposées égales.

11.2.1.1 Exemple

Vous avez mesuré la consommation d’oxygène de deux lots de poissons de même effectifs n=15 (un contrôle et un soumis au Ultra-sons)

##    Control   US
## 1     0.21 0.45
## 2     0.25 0.82
## 3     0.14 0.45
## 4     0.32 0.47
## 5     0.21 0.56
## 6     0.12 0.83
## 7     0.14 0.70
## 8     0.35 0.85
## 9     0.45 0.58
## 10    0.38 0.74
## 11    0.26 0.73
## 12    0.41 0.56
## 13    0.47 0.84
## 14    0.42 0.52
## 15    0.42 0.56

11.2.1.2 Conditions d’application

  • Normalité : Est-ce que les distributions suivent une loi normale? On utilise le test de Shapiro ou shapiro.test()
    • H0 la distribution observée est compatible avec la loi normale
    • H1 la distribution observée n’est pas conforme à la loi normale
shapiro.test(consom$Control)
## 
## 	Shapiro-Wilk normality test
## 
## data:  consom$Control
## W = 0.91927, p-value = 0.1877
shapiro.test(consom$US)
## 
## 	Shapiro-Wilk normality test
## 
## data:  consom$US
## W = 0.88742, p-value = 0.06132
  • Egalité des variances : Est-ce que les variances des échantillons sont égales? On utilise le test de Bartlett ou bartlett.test()
    • H0 Les variances sont égales
    • H1 Les variances diffèrent
bartlett.test(consom)
## 
## 	Bartlett test of homogeneity of variances
## 
## data:  consom
## Bartlett's K-squared = 0.59044, df = 1, p-value = 0.4422

Les conditions d’applications sont respectées!!

11.2.1.3 Calcul du test

  • Unilatéral ou bilatéral? C’est ici que vient votre connaissance en biologie. Normalement la consommation en oxygène est plus forte durant un stress, par conséquent, on veut savoir si la consommation moyenne des US est supérieure à celle des Contrôles.
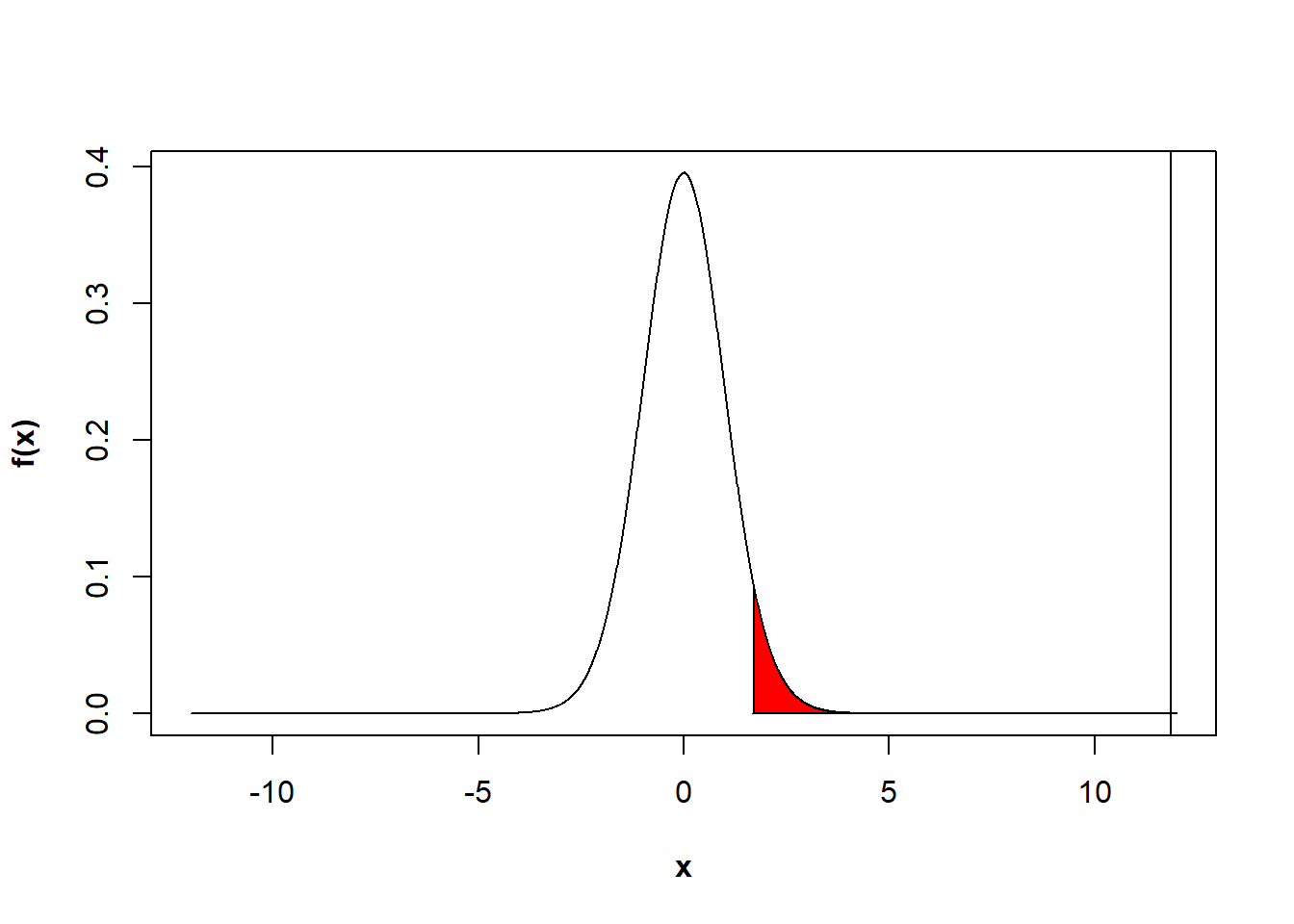
Fonction de densité associée à une loi de t de student à 29 ddl.

Figure 11.2: Fonction de densité associée à une loi de t de student à 29 ddl. 

t.test(consom,alternative="greater")
## 
## 	One Sample t-test
## 
## data:  consom
## t = 11.858, df = 29, p-value = 6.042e-13
## alternative hypothesis: true mean is greater than 0
## 95 percent confidence interval:
##  0.4057969       Inf
## sample estimates:
## mean of x 
## 0.4736667

11.2.2 Test U de Wilcoxon-Mann-Whitney (non paramétrique)

Lorsque la validité du test t n’est pas assurée, le test U en est la parade.

11.2.2.1 Exemple

Vous avez réalisé des bennes dans deux sites A et B ayant des granulométries différentes. Le site A est caractérisé par un sable hétérogène et le site B par une vase. Vous venez de passer 2 semaines à identifier les invertébrés et vous voulez savoir si le site A est moins dense que le site B.

##    Site  Ind
## 1     A   37
## 2     A   72
## 3     B 1200
## 4     B  504
## 5     A  321
## 6     B  173
## 7     A   49
## 8     A   18
## 9     B  856
## 10    A   50
## 11    B  274
## 12    B  168
## 13    A  102
## 14    A   49
## 15    A   20

On utilise la commande wilcox.test()

11.2.2.2 Calcul du test

Unilatéral ou bilatéral?

wilcox.test(Ind~Site,data=Ind.gran,alternative="less")
## 
## 	Wilcoxon rank sum test with continuity correction
## 
## data:  Ind by Site
## W = 3, p-value = 0.002786
## alternative hypothesis: true location shift is less than 0

Il y a bien une différence significative, le nombre d’individus est plus faible dans le site A que dans le site B.

11.3 Une variable et k échantillons

11.3.1 ANOVA : ANalysis Of VAriance (paramétrique)

L’ANOVA sert à faire des comparaisons de moyennes!!

L’ANOVA va permettre de comparer les écarts des moyennes entre plusieurs échantillons de distributions normales et de variances égales.

11.3.1.1 Exemple

Vous avez mesuré la concentration en Cadmium dans 3 populations de moules réparties sur le littoral normand afin de connaitre l’impact du relargage accidentelle de l’usine de métallurgie.

##   Population Conc_Cd
## 1          A  350.15
## 2          B  434.81
## 3          C  371.72
## 4          A  360.50
## 5          A  204.13
## 6          A  311.55

11.3.1.2 Conditions d’application

  • Normalité
shapiro.test(Contamination$Conc_Cd[Contamination$Population=="A"])
## 
## 	Shapiro-Wilk normality test
## 
## data:  Contamination$Conc_Cd[Contamination$Population == "A"]
## W = 0.97301, p-value = 0.7217
shapiro.test(Contamination$Conc_Cd[Contamination$Population=="B"])
## 
## 	Shapiro-Wilk normality test
## 
## data:  Contamination$Conc_Cd[Contamination$Population == "B"]
## W = 0.9609, p-value = 0.6192
shapiro.test(Contamination$Conc_Cd[Contamination$Population=="C"])
## 
## 	Shapiro-Wilk normality test
## 
## data:  Contamination$Conc_Cd[Contamination$Population == "C"]
## W = 0.96671, p-value = 0.5176
  • Egalité des variances
bartlett.test(Conc_Cd~Population,data=Contamination)
## 
## 	Bartlett test of homogeneity of variances
## 
## data:  Conc_Cd by Population
## Bartlett's K-squared = 2.0487, df = 2, p-value = 0.359

11.3.1.3 Calcul du test

On utilise la fonction aov() pour réaliser l’analyse de variance et anova() pour voir les résultats

Contam.aov <- aov(Conc_Cd~Population,data=Contamination)
anova(Contam.aov )
## Analysis of Variance Table
## 
## Response: Conc_Cd
##            Df  Sum Sq Mean Sq F value Pr(>F)
## Population  2   21236   10618  0.5166 0.5989
## Residuals  67 1377216   20556
Source de variation Degrés de liberté Somme des carrés Carrés moyens F p-value
Facteur (ou intergroupe) g-1 SCE \(CME=\frac{SCE}{g-1}\) \(\frac{CME}{CMR}\)
Résidus (ou intragroupe) n-g SCR \(CMR=\frac{SCR}{n-g}\)

11.3.2 Test H de Kruskall-Wallis (non paramétrique)

C’est une généralisation à g échantillons du test U

11.3.2.1 Hypothèses

  • H0 : La distribution des g échantillons est identiques
  • H1 : Il y au moins un distribution qui est différente de g-1 autres

11.3.2.2 Calcul du test

La fonction à utiliser est kruskal.test().

Reprenons l’exemple précédent:

kruskal.test(Conc_Cd~Population,data=Contamination)
## 
## 	Kruskal-Wallis rank sum test
## 
## data:  Conc_Cd by Population
## Kruskal-Wallis chi-squared = 1.4713, df = 2, p-value = 0.4792