9 Moyennes, variance et intervalle de confiance

9.1 Moyenne arithmétique vs. Moyenne géométrique

9.1.1 Moyenne arithmétique

La moyenne arithmétique est celle qui permet de calculer sa moyenne trimestielle. Elle consiste à diviser la somme des éléments par le nombre d’éléments. Elle est symbolisée par \(\overline{x}\) si elle est calculée sur les éléments d’un échantillon d’effectif n et \(\mu\) si elle est calculée sur la population entière d’effectif N.

\(\overline{x}= \sum_{i=0}^n \frac{x_{i}}{n}\) et \(\mu= \sum_{i=0}^N \frac{x_{i}}{N}\)

Si les données sont rangées en k classes dans un échantillon d’effectif n alors : \[ \overline{x}= \sum_{i=0}^k \frac{f_{i} x_{i}}{n}\]

9.1.2 Moyenne géométrique

La moyenne géométrique est utilisée lorsque les valeurs de x suivent une progression géométrique - une suite de nombres où on passe d’un terme au suivant en multipliant toujours par le même nombre. Cela peut-être la dose d’un composé que l’on double pour tester un traitement. La moyenne géométrique est surtout employée pour des variables qui suivent une échelle logarithmique. Elle s’écrit de la manière suivante : \[\overline{x_G}=\sqrt[n]{\prod_{i=0}^n x_i}\]

9.2 Variance et écart-type : Paramètres de dispersion

La variance - notée \(\sigma^2\) lorsqu’elle se rapporte à la population entière ou \(s^2\) si elle est une estimation calculée à partir d’un échantillon - correspond à l’écart à la moyenne au carré pour s’affranchir du signe et principalement pour faire apparaitre des propriétés mathématiques pour effectuer des tests statistiques.

\(\sigma^2=\frac{\sum_{i=1}^N (x_i-\mu)}{N}\) et \(s^2=\frac{\sum_{i=1}^n (x_i-\overline{x})}{n-1}\)

Pour \(s^2\) pourquoi mettre \(n-1\) au dénominateur et non pas \(n\)?
On utilise la dénominateur \(n-1\) pour la sous-estimation si \(n\) était au dénominateur. En effet, si on connaissait la valeur \(\mu\), on aurait une variance qui serait trop petite. Ainsi \(s^2\) sous-estime systématiquement \(\sigma^2\). Pour contre-balancer cet effet, il faut remplacer \(n\) par \(n-1\). Toutefois, plus \(n\rightarrow N\) (avec N très grand) plus \(s^2 \rightarrow \sigma^2\), la correction devient moins nécessaire.

Si les valeurs sont rangées en k classes alors la variance s’écrit : \[s^2=\frac{\sum_{i=1}^k n_i(x_i-\overline{x})}{n-1}\]

Quelques propriétés de la variance :

Si toutes les observations ont la même valeur, la variance est nulle.
Plus les valeurs sont dispersées plus la variance sera grande.
La variance est toujours positive ou nulle.
Un changement d’unités de \(x\) entraine une multiplication de \(\overline{x}\) par une constance \(c\), de \({s_x}^2\) par \(c^2\) et de \(s_x\) par c.

L’écart-type symbolisé par \(\sigma\) pour la population et \(s\) pour l’estimation à partir d’un échantillon est simplement la racine carré de la variance:

\(\sigma=\sqrt{\sigma^2}\) et \(s=\sqrt{s^2}\)

9.3 Intervalle de confiance

9.3.1 Intervalle de confiance de la moyenne

9.3.1.1 Paramétrique

Soit un population d’effectif \(N\) de moyenne \(\mu\) et de variance \(\sigma^2\). Dans cette population nous réalisons \(k\) échantillonnages de \(n\) éléments, les \(k\) échantillons ont donc les paramètres suivants : \(\overline{x_k}\) et \({s_k}^2\). La distribution des moyennes suit une loi normale \(N(\mu_{\overline{x}},s_{\overline{x}})\)) mais également à une loi de Student à n-1 degré de liberte (n-1 ddl) \(T(ddl)\). \(s_{\overline{x}}=\frac{s_x}{\sqrt{n}}\) est appelé l’erreur type et nous confirmerons ce résultat en TP par des simulations.

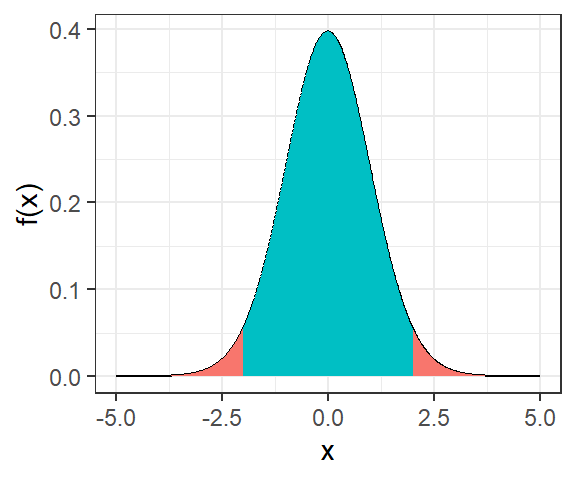
La figure suivante représente la distribution des moyennes d’une variable \(X\).

Les zones rouges correspondent à la probabilité d’obtenir \(X \notin [-x_{\frac{\alpha}{2}};x_{\frac{\alpha}{2}}]\) soit \(P(|X|>x_{\frac{\alpha}{2}})=\alpha\).
La zone bleu nous intéresse pour calculer l’intervalle de confiance car elle correspond à la probabilité d’obtenir \(X \in [-x_{\frac{\alpha}{2}};x_{\frac{\alpha}{2}}]\) soit \[P(-x_{\frac{\alpha}{2}}<X<x_{\frac{\alpha}{2}})=1-\alpha\]

\(\alpha\) correspond au risque de faire une erreur. Dans la communauté scientifique ont utilise généralement les seuils de 0.1%, 1% et 5%.

Pour comparer notre distribution des moyennes avec la distribution de Student (\(t\)), il va falloir centrer réduire notre distribution de moyennes. On crée ainsi une nouvelle variable: \[T=\frac{\overline{x}-\mu}{s_{\overline{x}}}\] On cherche donc : \[P(-t_{(\frac{\alpha}{2},n-1)}<T<t_{(\frac{\alpha}{2},n-1)})=1-\alpha\] ce qui équivaut à \[P(-t_{(\frac{\alpha}{2},n-1)}<\frac{\overline{x}-\mu}{s_{\overline{x}}}<t_{(\frac{\alpha}{2},n-1)})=1-\alpha\] \[P(\overline{x}-t_{(\frac{\alpha}{2},n-1)}s_{\overline{x}}<\mu<\overline{x}+t_{(\frac{\alpha}{2},n-1)}s_{\overline{x}})=1-\alpha\]

Sachant que \(s_{\overline{x}}=\frac{s_x}{\sqrt{n}}\), l’intervalle de confiance s’écrit :

\[P(\overline{x}-t_{(\frac{\alpha}{2},n-1)}\frac{s_x}{\sqrt{n}}<\mu<\overline{x}+t_{(\frac{\alpha}{2},n-1)}\frac{s_x}{\sqrt{n}})=1-\alpha\]

9.3.1.2 Par bootstrap non paramétrique

Le bootstrap non paramétrique repose sur l’hypothèse que la meilleure information que l’on possède sur la distribution de X est celle de l’échantillon.

Si l’échantillon est issu d’un échantillonnage aléatoire simple alors sa composition devrait refléter celle de la population, par conséquent la distribution des données devrait s’approcher de celle de la population.

Le bootstrap consiste à produire \(K\) pseudo-échantillons en faisant un tirage aléatoire AVEC remise. Pour chaque échantillon, on calcule la moyenne, et avec les \(K\) moyennes on peut faire une distribution. On prend les pourcentiles qui correspondent à l’intervalle de confiance recherché dans cette distribution.

Exemple :

Si \(n\)=10000 et \(\alpha\)=0.5 alors on prend la 250^^ième^ et la 9750^^ième^ valeurs. On obtient l’interalle à 95%.

9.3.2 Intervalle de confiance de la variance et de l’écart-type

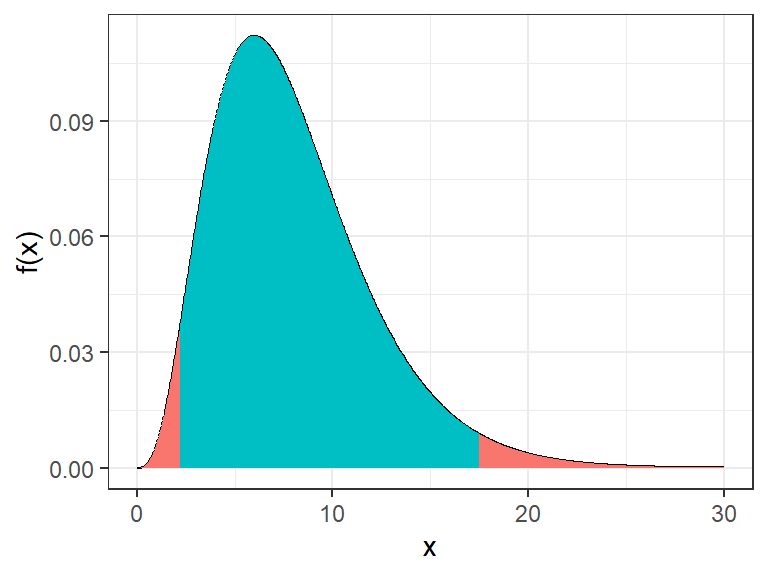
Soit un échantillon d’effectif \(n\) La distribution de la variance suit la distribution du \(\chi^2\) à \(n-1\) ddl car on se base sur l’estimation de la moyenne \(\overline{x}\) et non sur la moyenne de la population \(\mu\).

La zone bleu nous intéresse pour calculer l’intervalle de confiance car elle correspond à la probabilité d’obtenir \(X \in [{\chi^2}_{1-\frac{\alpha}{2}};{\chi^2}_{\frac{\alpha}{2}}]\) soit \[P({\chi^2}_{1-\frac{\alpha}{2}}<X<{\chi^2}_{\frac{\alpha}{2}})=1-\alpha\]

L’intervalle de confiance de la variance est donnée par :

\[P(\frac{(n-1){s_{x}}^2}{{\chi^2}_{(n-1,\frac{\alpha}{2})}}\le\sigma^2\le \frac{(n-1){s_{x}}^2}{{\chi^2}_{(n-1,1-\frac{\alpha}{2})}})=1-\alpha\]

L’intervalle de confiance de l’écart-type est donnée par :

\[P(\sqrt\frac{(n-1){s_{x}}^2}{{\chi^2}_{(n-1,\frac{\alpha}{2})}}\le\sigma\le \sqrt\frac{(n-1){s_{x}}^2}{{\chi^2}_{(n-1,1-\frac{\alpha}{2})}})=1-\alpha\]

9.3.3 Ajustement de la taille d’un échantillon en fonction de la variance.

Dans le cadre d’échantillonnage avec une méthode aléatoire, plus la taille de l’échantillon est grande, plus l’analyse sera précise. Ce qui parait logique. Mais la proportionnalité n’est pas vrai. L’analyse ne sera pas 2 fois plus précise, si votre échantillon est 2 fois plus important.

Il est important d’appréhender le fait que la taille de l’échantillon n’est pas en lien avec la taille de la population.

La détermination de la taille de l’échantillon est donc une étape importante avant toute enquête, qui est l’occasion d’arrêter la précision de l’analyse (budget alloué, temps).

\[n=\frac{t_{(\alpha,\infty)}^2 s^2}{m^2}\]

avec \(s^2\) la variance de l’échantillon et \(m\) la marge d’erreur.