4 Présentation des données

Pourquoi un chapitre sur la présentation de données car sur Excel ou Calc on peut faire tous les graphiques que l’on veut… . Hmmm d’accord mais êtes-vous sûr que :

vous avez choisi la bonne représentation pour expliquer vos données?
votre figure est complète (titre des axes, légende,…)?
vous interprétez bien votre figure ?

Bref, il est très facile de faire une figure, mais il l’est moins quand on veut véhiculer une idée, un résultat. Le choix de la représentation est une étape cruciale qui améliorera grandement la compréhension de vos rapports, présentations…

4.1 Un jeux de données : Croissance de Coquille Saint-Jacques

4.1.1 Contexte

Dans une ferme d’élevage de Coquille Saint-Jacques (Pecten maximus, 4.1), le responsable production veut savoir si les individus sont stressés lors des changements des mixtures alimentaires. Pour cela, il dispose de 4 bassins dans lesquels il y a 50 individus. Dans 2 bassins, il change la composition en phytoplancton de la nourriture. Les deux derniers servent de contrôle, la composition spécifique en phytoplancton n’est pas changée. Il mesure le taux de croissance spécifique exprimé en pourcentage et l’activité valvaire.

Pour information :

Embranchement : Mollusca

Classe : Bivalve

Ordre : Pectinida

Famille : Pectinidae

Genre : Pecten

Espèce : Pecten maximus

Figure 4.1: Coquille Saint-Jacques (Pecten maximus) dans son habitat naturel

4.1.2 Les variables

Avant toute chose, il est INDISPENSABLE de décrire les variables,i.e de définir le type mathématique de chaque variable. Cela va fortement influencer le choix de la représentation graphique. Pour cela, vous n’avez qu’à faire un tableau de synthèse :

Variables	Unité ou Etats	Type mathématiques
Bassin	A, B, C, D	Qualitative
Stress	O/N	Binaire
Activité valvaire	Bcp / Moy / Peu	Semi-quantitative
Température	°Celcius	Quantitative
Taux de croissance spécifique sur 2 mois	%	Quantitative

Voici le descriptif des variables dans R :

class(SGR.Coq)

## [1] "tbl_df"     "tbl"        "data.frame"

str(SGR.Coq)

## tibble [28 x 5] (S3: tbl_df/tbl/data.frame)
##  $ bassin     : chr [1:28] "A" "A" "A" "A" ...
##  $ stress     : chr [1:28] "O" "O" "O" "O" ...
##  $ act_valv   : chr [1:28] "Bcp" "Moy" "Peu" "Moy" ...
##  $ temperature: num [1:28] 13.6 13.6 16.3 12.2 12.3 ...
##  $ SGR_2mois  : num [1:28] 26.3 33 22 25.9 32 ...

summary(SGR.Coq)

##     bassin             stress            act_valv          temperature   
##  Length:28          Length:28          Length:28          Min.   :12.20  
##  Class :character   Class :character   Class :character   1st Qu.:13.16  
##  Mode  :character   Mode  :character   Mode  :character   Median :13.78  
##                                                           Mean   :14.26  
##                                                           3rd Qu.:14.64  
##                                                           Max.   :21.51  
##    SGR_2mois     
##  Min.   : 9.611  
##  1st Qu.:21.424  
##  Median :26.092  
##  Mean   :27.987  
##  3rd Qu.:36.258  
##  Max.   :47.217

4.2 Les séries statistiques simples

Une série statistique simple se compose des mesures d’une seule variable. Cette variable peut être quantitative ou qualitative (ordonnée ou non).

4.2.1 Les variables qualitatives

On décrit une variable qualitative par le nombre de fois q’un état est observé, on obtient alors l’occurence de chaque état. Dans notre exemple la variable act_valv présente 0 états. Voici l’ocurrence des 4 états :

table(SGR.Coq$act_valv)

## 
## Bcp Moy Peu 
##   6  12  10

4.2.1.1 Comment les quantifier?

Il existe 4 manières de quantifier l’importance d’un état par rapport à un autre :

La fréquence absolue correspond au nombre d’élément dans chaque modalité \[\sum{f_i}=n\]

summary(SGR.Coq[,1:3])

##     bassin             stress            act_valv        
##  Length:28          Length:28          Length:28         
##  Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character

La fréquence relative correspond à l’effectif absolu divisé par l’effectif total. \[\sum{frel_i}=1\] \[frel_i= \frac{f_i}{n}\]

SGR.Coq.table <- table(SGR.Coq$act_valv)
SGR.Coq.frel <- table(SGR.Coq$act_valv)/sum(SGR.Coq.table)
SGR.Coq.frel <- round(SGR.Coq.frel,2)
SGR.Coq.frel

## 
##  Bcp  Moy  Peu 
## 0.21 0.43 0.36

sum(SGR.Coq.frel)

## [1] 1

Le pourcentage correspond à l’effectif relatif multiplié par 100. \[\sum{pourc_i}=100\] \[pourc_i= frel_i\times 100\]

SGR.Coq.pourc <- SGR.Coq.frel*100
SGR.Coq.pourc

## 
## Bcp Moy Peu 
##  21  43  36

sum(SGR.Coq.pourc)

## [1] 100

La fréquence cumulée d’une modalité correspond à la somme de son propre effectif et de celui des modalités ayant des effectifs plus petits

cumsum(sort(SGR.Coq.table))

## Bcp Peu Moy 
##   6  16  28

cumsum(sort(SGR.Coq.frel))

##  Bcp  Peu  Moy 
## 0.21 0.57 1.00

cumsum(sort(SGR.Coq.pourc))

## Bcp Peu Moy 
##  21  57 100

4.2.1.2 Les représentations graphiques

Pour représenter des variables qualitatives ordonnées ou non et binaire, il sera préférable de choisir le diagramme en bâton (ou barplot). En abscisse on retrouve les différents états de la variable qualitative et en ordonnée les fréquences (relatives, absolues ou cumuluées) ou les pourcentages. Sauf si la variable est semi-quantitative, les étiquesttes des abscisses ne sont pas ordonnées.

Voici le diagramme en bâton correspondant à la distribution relatives des modalités de la variable act_valv:

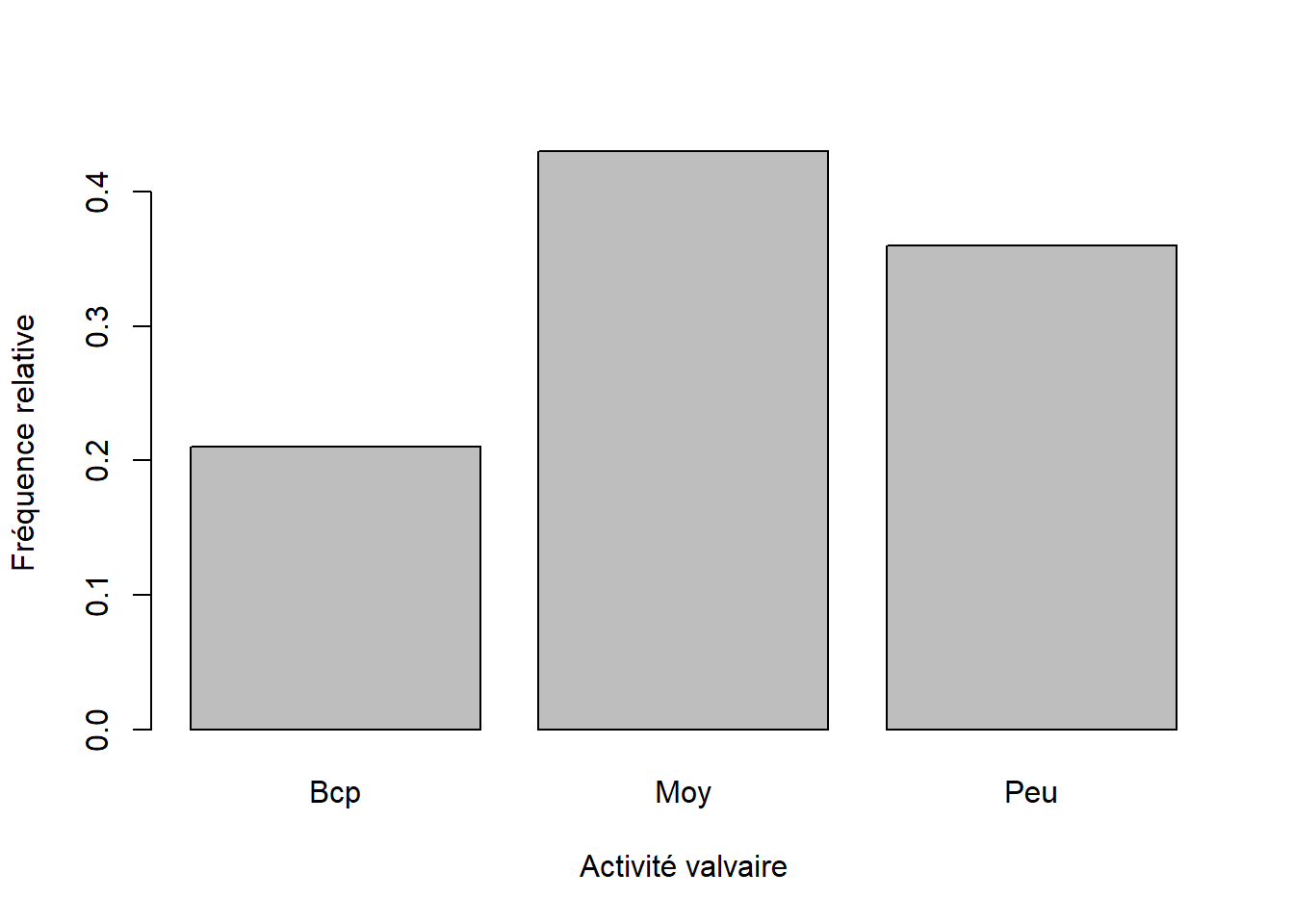
barplot(SGR.Coq.frel,xlab="Activité valvaire",ylab="Fréquence relative")

Par contre, je vous DECONSEILLE FORTEMENT d’utiliser le “camembert” pour représenter ce type de variable. Voici un exemple pour illustrer mon propos :
Vous avez étudié la structuration bio-sédimentaire de 3 stations de la baie de Tah’Malou dans la province de Bobohlà. Pour représenter cette distribution vous avez choisi “le camembert” (Figure 2) :

Distribution bio-sédimentaire dans 3 stations de la baie de Tah'Malou (A5.1 Sable fin; A5.2 Sédiment grossier; A5.3 Vase; A5.4 Sédiment hétérogène)

Figure 4.2: Distribution bio-sédimentaire dans 3 stations de la baie de Tah’Malou (A5.1 Sable fin; A5.2 Sédiment grossier; A5.3 Vase; A5.4 Sédiment hétérogène)

Que pouvez-vous en conclure? Eh oui pas beaucoup de choses…. Vous ne voyez pas de grandes différences entre ces graphiques, vous ne pouvez pas vous appuyer sur des valeurs. Et maintenant si je vous rajoute ce graphique (Figure 3)?

Figure 4.3: Distribution bio-sédimentaire dans 3 stations de la baie de Tah’Malou (A5.1 Sable fin; A5.2 Sédiment grossier; A5.3 Vase; A5.4 Sédiment hétérogène)

AAhhh là on peut commencer à discuter!!! Les diagrammes en bâtons permettent de visualiser plus d’informations et de visualiser les différences. L’oeil humain estime très bien les distances linéaires mais estime très mal les surfaces relatives. Le camembert peut aisément être remplacé par des diagrammes en bâton ou des histogrammes. Je ne veux voir dans aucun(e)s de vos rapports et de vos présentations orales un camembert!!!

4.2.2 Les variables quantitatives

S’il est simple de représenter les variables qualitatives car les classes correspondent aux différents états de la variable. Pour les variables quantitatives c’est un peu plus complexes; si on applique la même méthode que précédemment ce sera facile pour un petit échantillon n<10 mais si l’échantillon est plus grand le graphique deviendra rapidement illisible. Il devient donc important de créer des classes (intervalles), on discrétise alors la variable quantitative.
Mais alors combien de classes choisir? quelle amplitude pour chaque classe?

4.2.2.1 La discrétisation des variables qualitatives

Il existe des règles qui permettent de choisir un nombre approprié de classe. En discrétisant les variables quantitatives on obtient des variables semi-quantitatives, on a donc perdu un peu d’information. Ces règles permettent d’obtenir un juste compromis entre la perte d’information et la meilleure représentation.

Régle de Sturge de Herbert Sturge (1926): \[nombre\ de\ classe=1+(3.3\times log(n))\] où n est l’effectif de l’échantillon, et log(n) le logarithme en base 10 de l’effectif de l’échantillon.

La construction de la formule se base sur une distribution symétrique, de distribution binomiale ou gaussienne. Pour peu que les données à représenter ne suivent pas cette forme, le nombre de tranches n’a plus de justification.

Dès que les données d’échantillon ont une distribution asymétrique, ou présentant des valeurs largement étalées, il est préférable de choisir la règle de Yule :

Régle de Yule : \[nombre\ de\ classe=2.5 \sqrt[4]{n})\]

Les règles de Sturge et de Yule sont basées uniquement sur l’effectif de l’échantillon. Il est important de vérifier que votre variable ne comporte pas de valeurs extrêmes ce qui risque de fausser le calcul du nombre de classe.

L’intervalle de chaque classe est le rapport entre l’étendue de variation et le nombre de classe :

\[Int_{classe}=\frac{max-min}{nombre\ de\ classe}\]

4.2.2.2 Un exemple d’application

Voici la distribution du poids (en gramme) de deux populations (A et B)de Turbot commun (Scophthalmus maximus). 40 individus ont été échantillonnés dans la population A et 65 dans la population B.

Distribution du poids deux populations de turbot commun (*Scophthalmus maximus*)
	Pop A	Pop B
Minimum	5	10
1^er quartile	110	550
Médiane	358	788
3^ème quartile	612.75	1134
Maximum	1015	2267

Nombre de classes

Population A : 1+3.3*log(40) = 6
Population B : 1+3.3*log(65) = 7

Etendue de variation

Population A : 1015-5 = 1010g
Population B : 2267-10 = 2257g

Intervalle de classe

Population A : 1010 / 6 = 161g
Population B : 2257 / 7 = 323g

4.2.2.3 La représentation graphique

Afin de représenter la distribution de fréquence d’une variable quantitative, l’histogramme est le plus adapté. Les barres verticales représentent la fréquence de chacune des classes. Contrairement au diagramme en bâton, les barres se touchent car la variable est continue à l’échelle de la variation de la variable.

hist(popA,xlab="Poids (en gramme)",ylab="Fréquence absolue",breaks=6,main="")

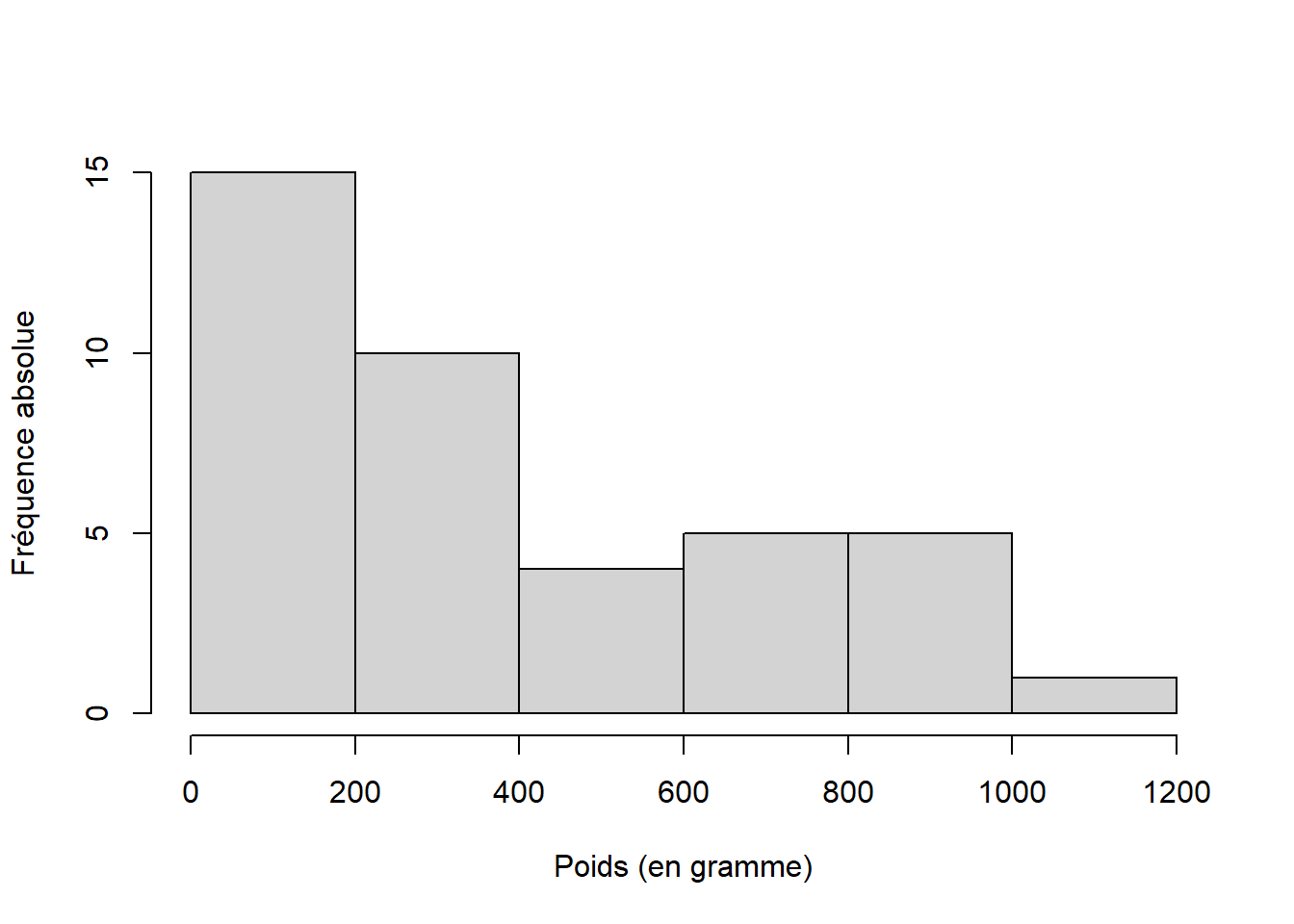
Histogramme de la distribution de fréquence absolue du poids(en g) des 65 turbots communs (*Scophthalmus maximus*) échantillonnés dans la population A.

Figure 4.4: Histogramme de la distribution de fréquence absolue du poids(en g) des 65 turbots communs (Scophthalmus maximus) échantillonnés dans la population A.

hist(popB,xlab="Poids (en gramme)",ylab="Fréquence absolue",breaks=7,main="")

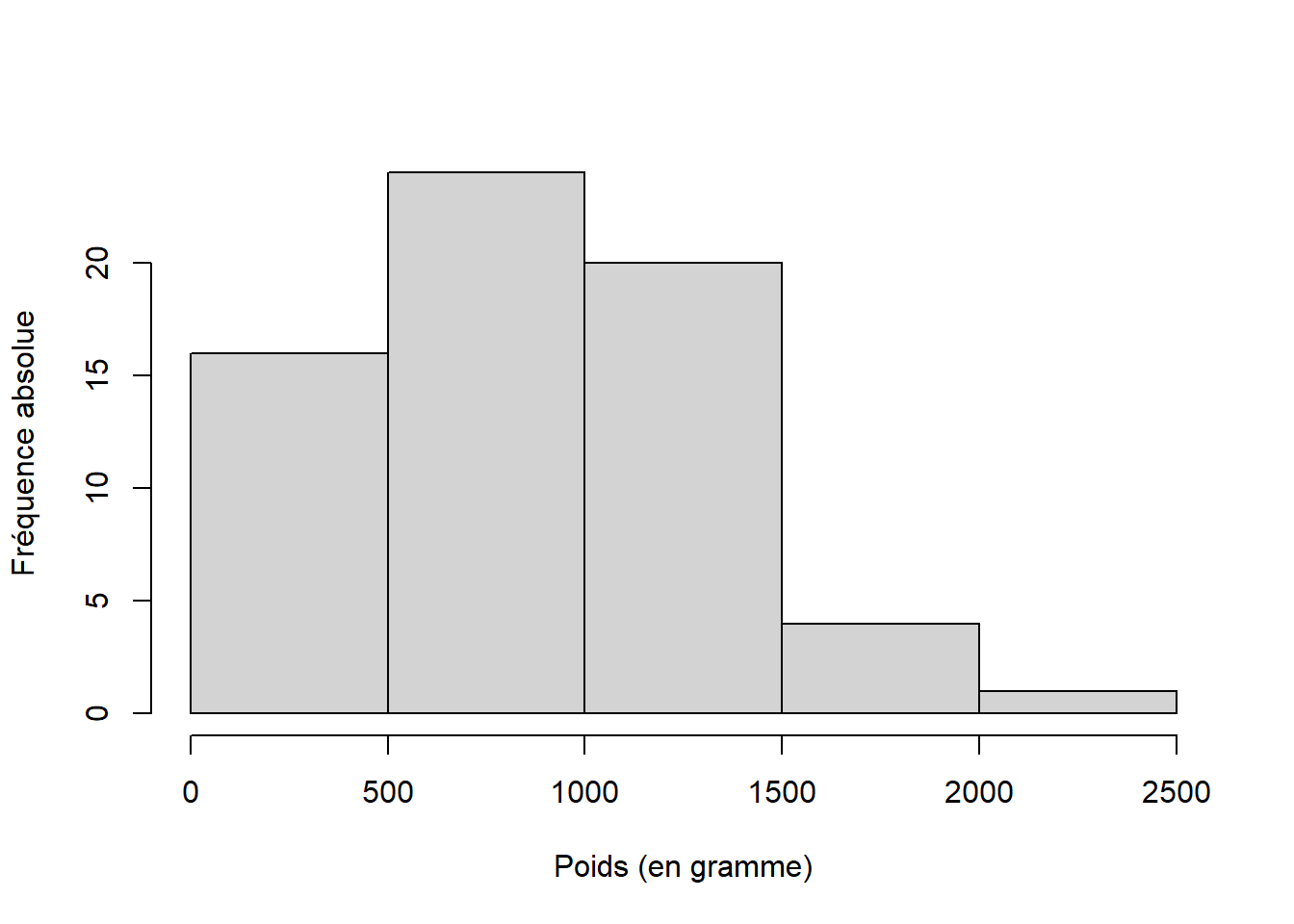
Figure 4.5: Histogramme de la distribution de fréquence absolue du poids(en g) des 65 turbots communs (Scophthalmus maximus) échantillonnés dans la population B.

Vous noterez que R ne respecte pas tout à fait le nombre de classe défini dans l’argument breaks. Le logiciel ajuste plus précisément le nombre de classe en fonction de la dispersion des valeurs. Ainsi, R aura tendance a augementer le nombre de classe pour optimiser le compromis entre information et lisibilité.

Le polygone de fréquence est également une autre représentation pour les variables quantitatives. Les fréquences de chaque classe sont reliées entre elles par le milieu de la classe(mid). Ce polygone est refermé en ajoutant de part et d’autre une classe d’effectif 0.

popA.hist <- hist(popA,breaks=6,plot = F)
diff.mid <- unique(diff(popA.hist$mids))
k <- length(popA.hist$mids)
freq.popA.poly <- c(0,popA.hist$counts,0)
mids.popA.poly <- c(popA.hist$mids[1]-diff.mid,popA.hist$mids,popA.hist$mids[k]+diff.mid)
plot(mids.popA.poly ,freq.popA.poly,type="b",xlab="Poids (en g)",ylab="Fréquence absolue")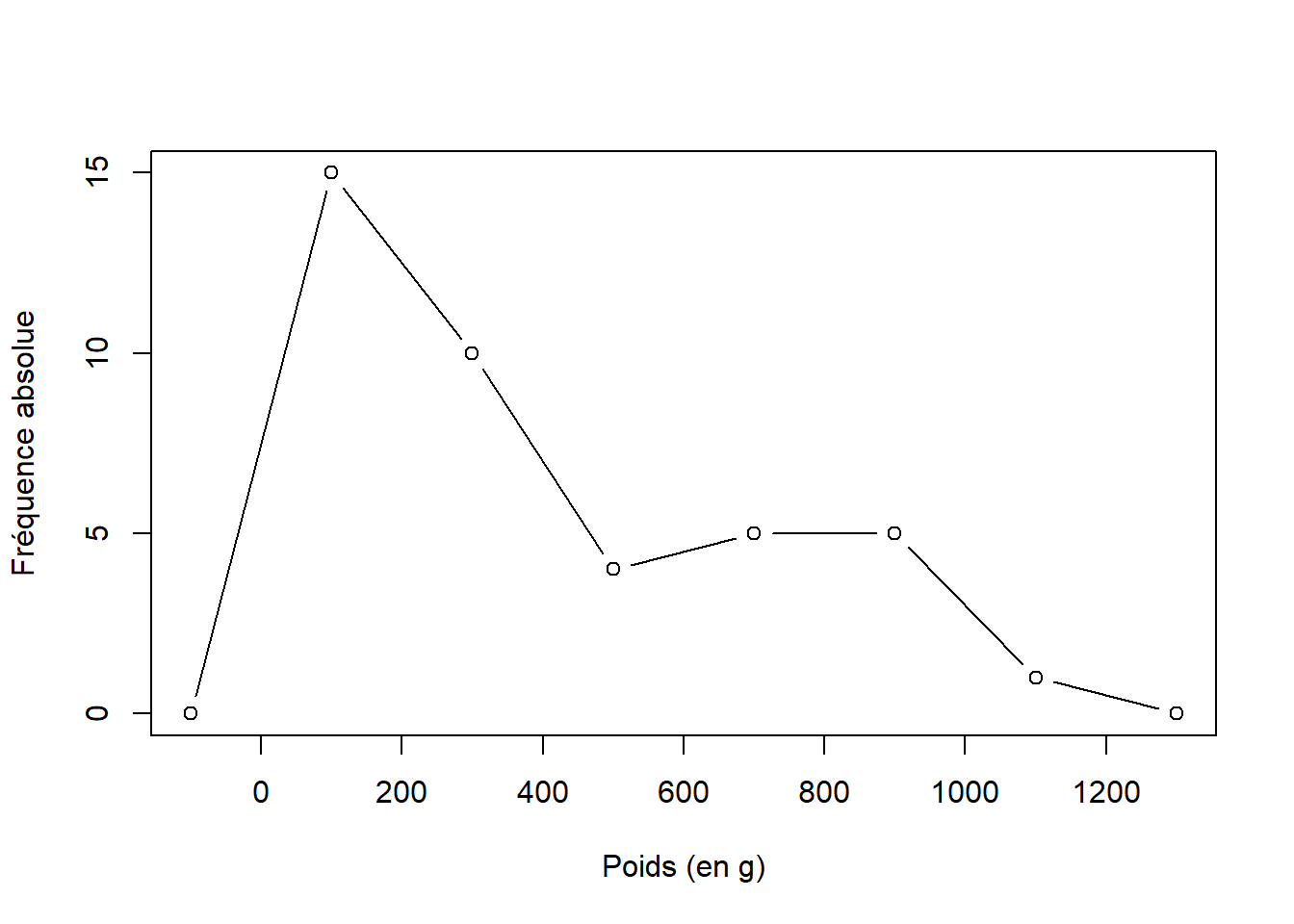

Polygone de fréquence de la distribution de fréquence absolue du poids(en g) des 65 turbots communs (*Scophthalmus maximus*) échantillonnés dans la population A.

Figure 4.6: Polygone de fréquence de la distribution de fréquence absolue du poids(en g) des 65 turbots communs (Scophthalmus maximus) échantillonnés dans la population A.

4.2.2.4 Une variable quantitative et plusieurs échantillons

Si vous souhaitez connaitre la distribution de vos mesures entre plusieurs échantillons la solution est la boîte à moustache.

Description d’une boîte à moustache

Q1 est la plus petite valeur de la série telle qu’au moins 25% des valeurs soient inférieures ou égales à Q1
Q3 est la plus petite valeur de la série telle qu’au moins 75% des valeurs soient inférieures ou égales à Q3
Ecart inter-quartile est \(Q3-Q1\)
La longueur maximal des moustaches est égale à \(1.5 \times(Q3-Q1)\)
Les «outliers» correspondent aux valeurs strictement supérieures à la longueur maximale des moustaches

On va reprendre notre exemple précédent sur la coquille Saint-Jacques de la partie 1. La croissance a été mesurée dans les 4 bassins, il est donc intéressant de connaitre la distribution des valeurs pour chaque bassin. On pourrait faire des polygones de fréquences superposés mais cela deviendrait rapidement illisible.

boxplot(SGR.Coq$SGR_2mois~SGR.Coq$bassin,xlab="Bassins",ylab="SGR (2mois)")

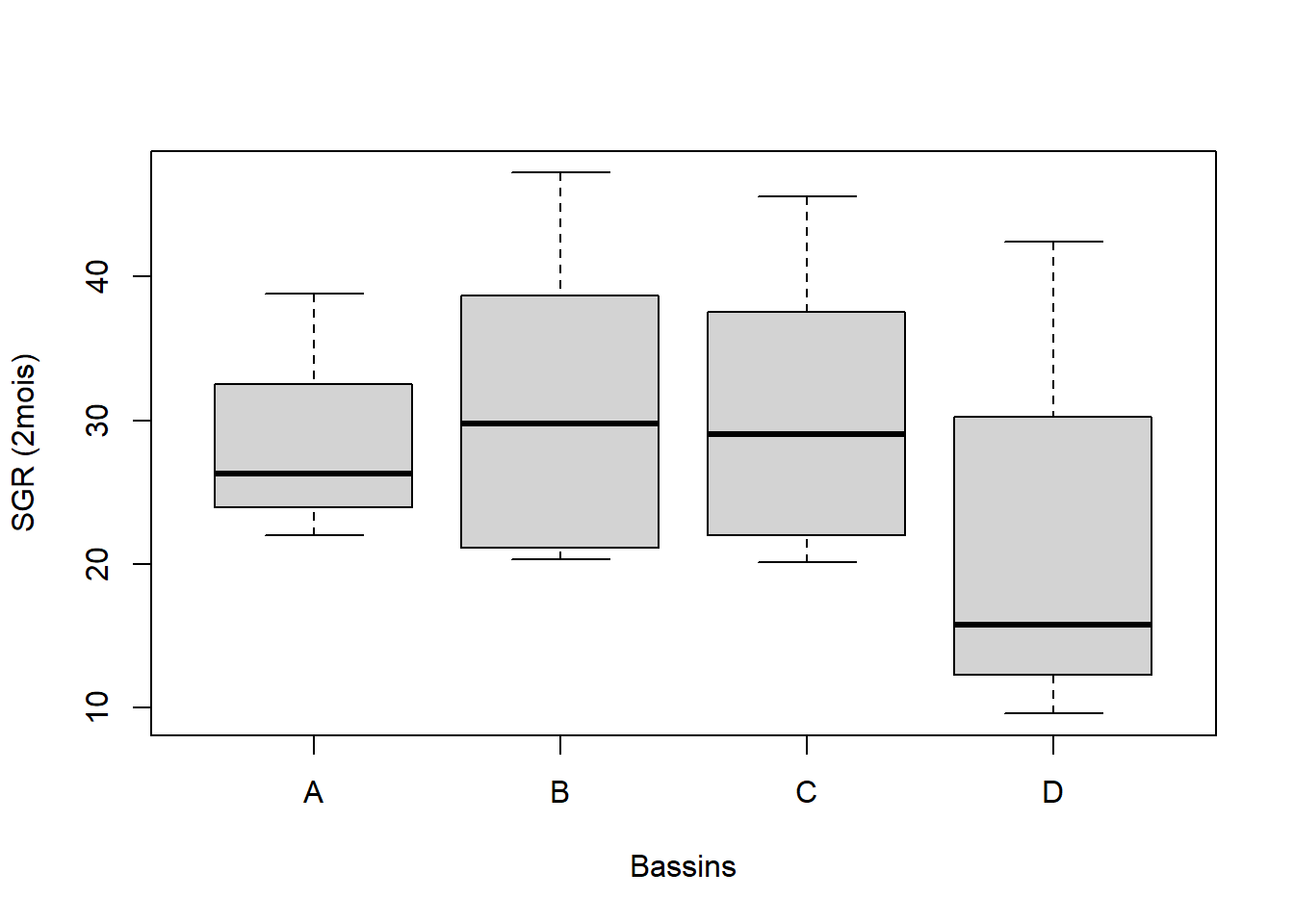
Figure 4.7: Diagramme à moustache de la distribution de la température dans les 4 bassins expérimentaux (A, B, C, D)

4.3 Les séries statistiques doubles

Un série statistique double se compose des mesures de deux variables.

4.3.1 Deux variables qualitatives

Pour représenter deux variables qualitatives on utilise un tableau de contingence, i.e. un tableau à deux entrées où les éléments sont rangées en fonction des états qu’ils prennent pour chacune des variables. Ce tableau est la base du test de \(\chi^2\). Si l’une des variables est semi-quantitative, on parle alors de tableau de corrélation de rang.

table(SGR.Coq$bassin,SGR.Coq$act_valv)

##    
##     Bcp Moy Peu
##   A   2   3   2
##   B   2   4   1
##   C   2   3   2
##   D   0   2   5

4.3.2 Une variable quantitative et une variable qualitative

####Distribution des valeurs

Si vous souhaitez observer la distribution des valeurs entre les différents états de la variable quantitative, la représentation la plus approprié est le diagramme à moustache. (cf section 2.3).

####Comparaison des moyennes

Dans le cas où vous souhaitez étudier l’effet d’une variable ou facteur, vous devrez choisir le diagramme en bâton en représentant en ordonnée les moyennes et les écarts-types. Nous traiterons le calcul des moyennes et des écarts-types et les tests statistiques de comparaison de moyennes dans le prochain cours et durant votre 3^ème année.

4.3.3 Deux variables quantitatives

Pour représenter le lien entre deux variables quantitatives, i.e. savoir si les variables évoluent dans le même sens, dans des sens opposés ou sont indépendantes l’une de l’autre, le diagramme de dispersion est le plus adéquate. L’une des variables est en ordonnée et l’autre en abscisse. Les deux variables doivent avoir le même nombre d’observations (ou mesures)

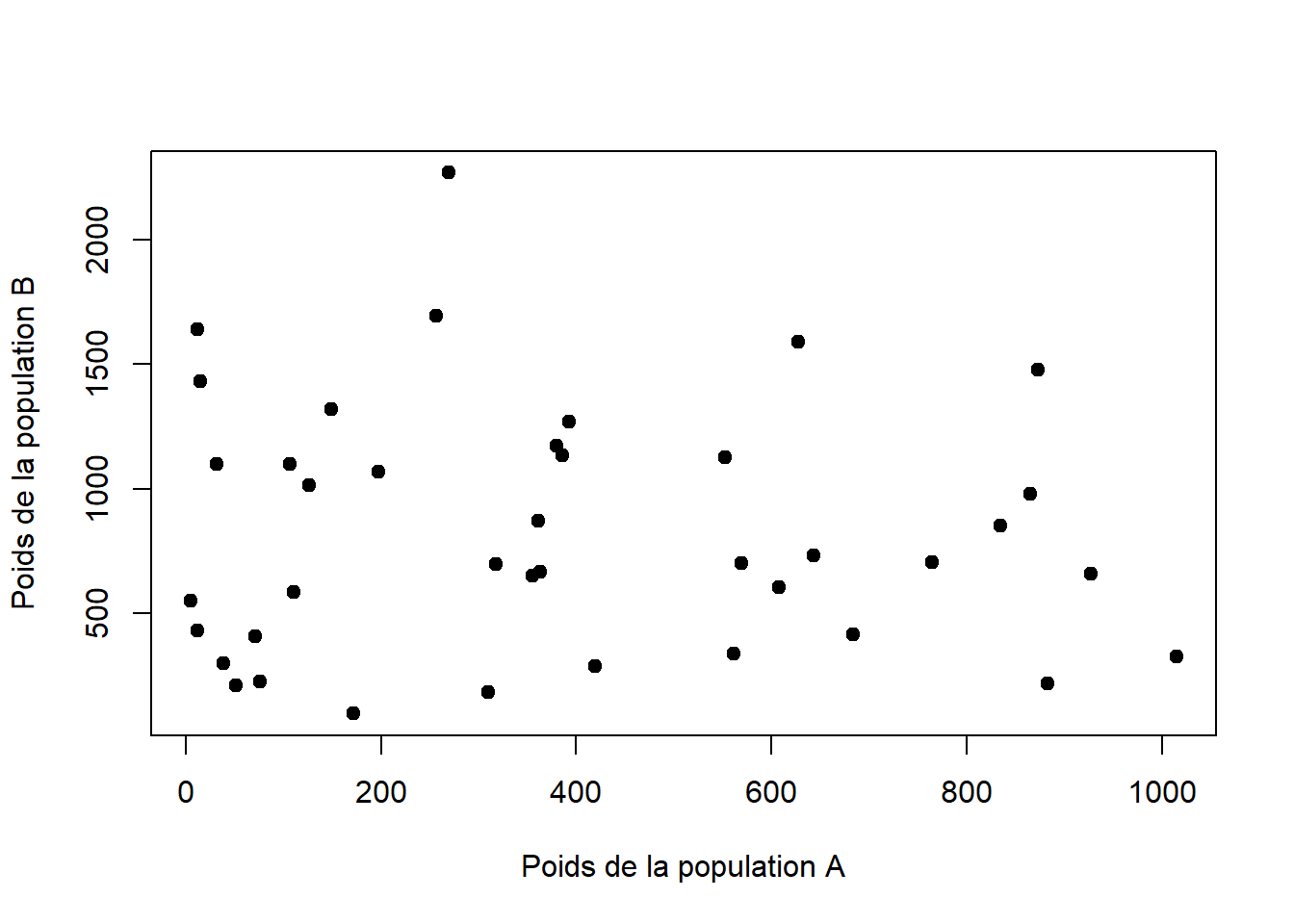
plot(popA,popB[1:40],xlab="Poids de la population A",ylab="Poids de la population B", pch=19)

Nous verrons dans le prochain cours, comment quantifier le lien entre deux variables quantitatives en utilisant les coefficients de corrélation.

4.4 Synthèse

	Diagramme à bâtons	Camembert	Histogramme	Polygone de fréquence	Diagramme à moustache	Diagramme de dispersion
1 variable qualitative	OK	JAMAIS
1 variable quantitative		JAMAIS	OK
1 quantitative / 1 qualitative	OK (si moyenne)	JAMAIS		OK	OK
2 qualitatives		JAMAIS		OK
2 quantitatives		JAMAIS		OK⁺	OK⁺	OK

⁺ : La/les variable(s) sont transformées en variables semi-quantitatives, par conséquent il y a une perte d’information.