8 Lois de distribution

8.1 Définitions

Distribution de probabilité correspond aux probabilités associées à une valeur ou un intervalle d’une variable aléatoire X

La fonction de masse est lié aux variables discrètes et donne la probabilité qu’une variable aléatoire X soit EGALE à une valeur x. \[f_m(x)=(X=x)\]

La fonction de densité est lié aux variables continues et donne la probabilité qu’une variable aléatoire X soit COMPRISE dans un intervalle $[a, b[$. \[\int_a^b f(x)dx = P(a\le X < b)=1\]

Exemple :

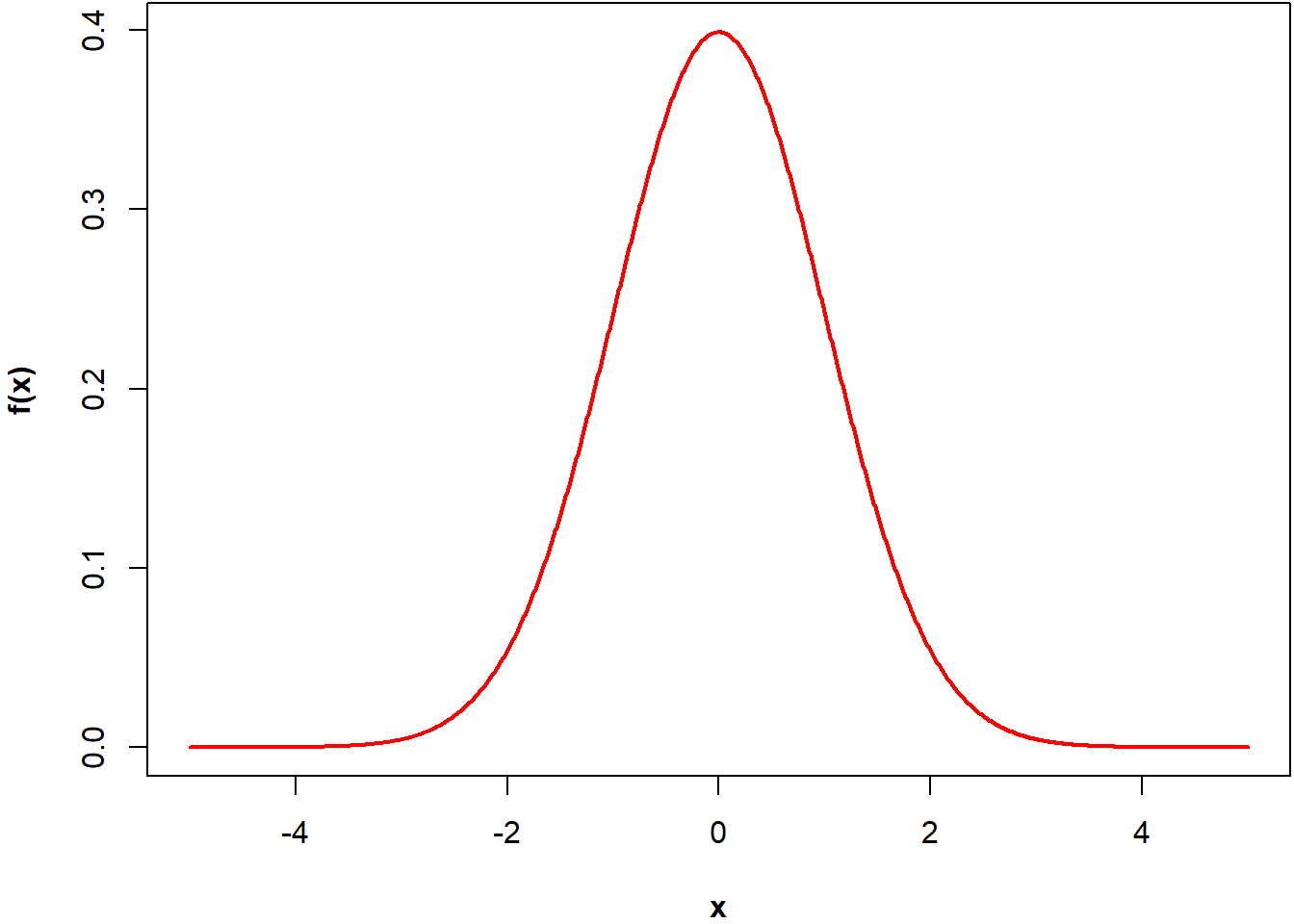
Figure 8.1: Fonction de densité de probabilité d’une loi normale centrée réduite

La fonction de répartition est la distribution cumulée de $f(x)$. Elle donne, pour tout réel x, la probabilité que X soit inférieure ou égale à x. Elle permet de définir la loi de distribution de la variable aléatoire X. \[F(X)=\int_{-\infty}^x f(x)dx = P(X \le x)\] \[1-F(X) = P(X > x)\] \[F(b)-F(a)=P(a\le X \le b)\]

Exemple :

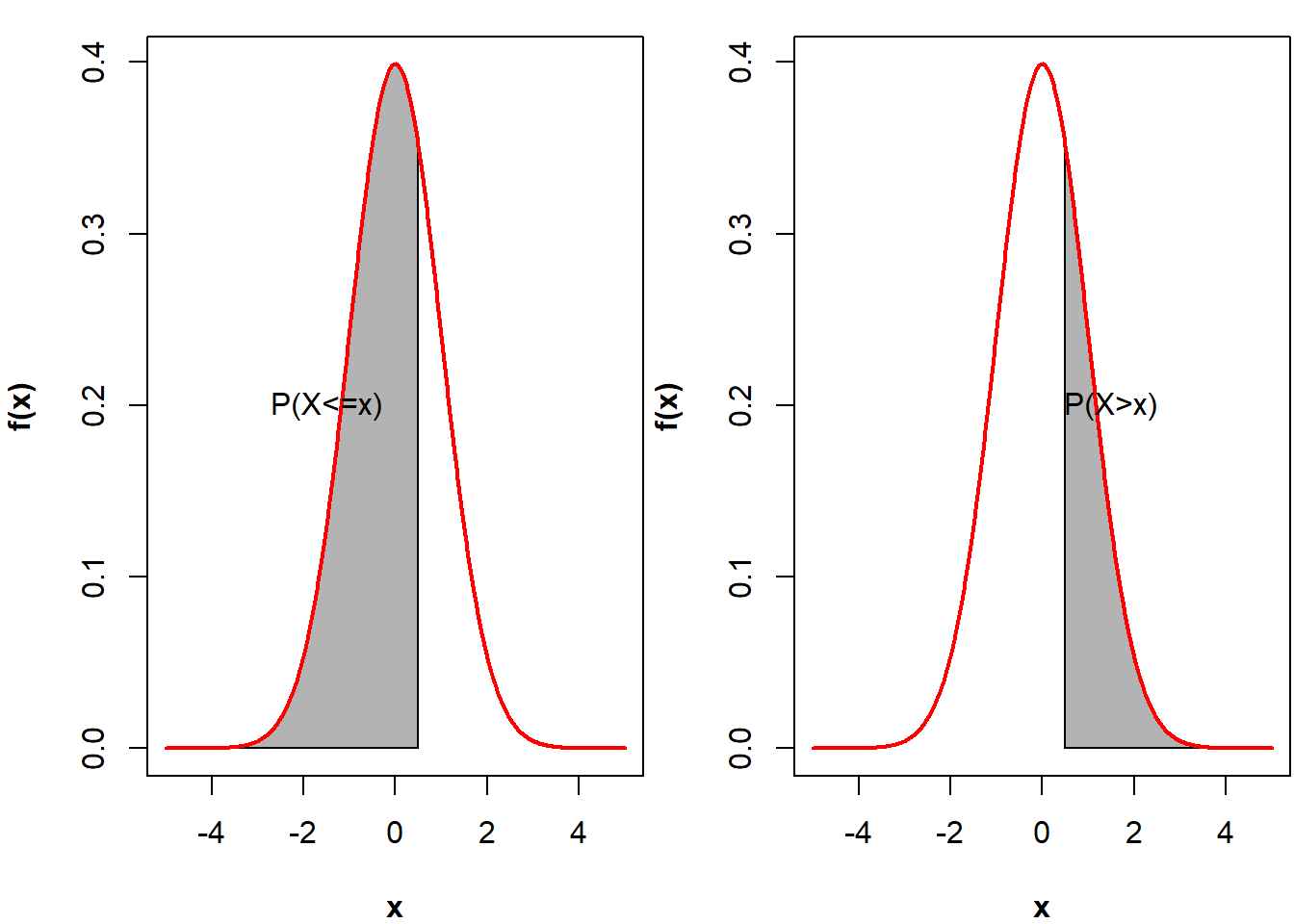
$Fonction de répartition d'une loi normale centrée réduite avec à gauche $F(X)=P(X \le x)$ et à droite $1-F(X)=P(X > x)$$

Figure 8.2: Fonction de répartition d’une loi normale centrée réduite avec à gauche $F(X)=P(X \le x)$ et à droite $1-F(X)=P(X > x)$

8.2 Lois de probabilité discontinues

8.2.1 La loi binomiale

Type de variable : Variables binaires

Description : La loi donne la probabilité d’obtenir k fois le résultat A quand n tirages sont réalisés.

Elle s’écrit $B(n,p)$

avec n : nombre de tirages
p : probabilité associée au résultat A

Exemple : Quelle est la probabilité d’avoir 2, 5, 15, 20 poissons vivants dans un bassin de 100 poissons sachant que $P_{vivant}=P_{mort}=\frac{1}{2}$.

dbinom(c(2,5,15,20),size=100,prob=0.5)

## [1] 3.904861e-27 5.939138e-23 1.998488e-13 4.228163e-10

8.2.2 La loi de Poisson

Type de variable : Variables binaires

Description : C’est une limite de la binomiale quand $p\rightarrow 0$ et $n \rightarrow \infty$. “Loi des évènements rares”

Elle s’écrit $P(np)$ ou $P(\lambda)$

avec n : nombre de tirages
p : probabilité associée au résultat rare

Tableau 1: Exemples d’application de la loi de Poisson.

Epreuve	Succès	Echec	p	n	Variable aléatoire X
Capture d’un poisson dans un filet	Espèce rare	Espèce commune	<0.001	Nombre de captures	Nombre de poissons d’espèces rares
Effet d’un contaminent	Mort	Survie	0.005	Nombre d’organismes contaminés	Nombre d’organismes morts
Erreur de saisie	Mauvaise frappe	Bonne frappe	0.001	Nombre de données	Nombre de données avec des erreurs

Exemple : Dans une benne Van Veen, vous constatez seulement 6 individus d’un polychète Nereis diversicolor sur un effectif total de 100 individus.

Quelle est la probabilité vous en échantillonnées exactement 10 individus avec 5 bennes?

p <- 0.06 
n <- 5
lambda <- n*p
lambda

## [1] 0.3

dpois(10,lambda)

## [1] 1.205483e-12

Quelle est la probabilité vous ayez au plus 8 individus dans 10 bennes?

p <- 0.06 
n <- 10
lambda <- n*p
lambda

## [1] 0.6

dpois(x=0:8,lambda = 6)

## [1] 0.002478752 0.014872513 0.044617539 0.089235078 0.133852618 0.160623141
## [7] 0.160623141 0.137676978 0.103257734

sum(dpois(x=0:8,lambda = 6))

## [1] 0.8472375

8.3 Lois de probabilité continues

8.3.1 La loi Normale

Type de variable : Variables continues

Description : la fonction de densité $f(x)$ est toujours positives, la courbe est symétrique,i.e. la médiane, la moyenne et le mode sont confondus.

Elle s’écrit $N(\mu,\sigma)$

avec $\mu$ : moyenne de la distribution
$\sigma$ : écart-type de la distribution

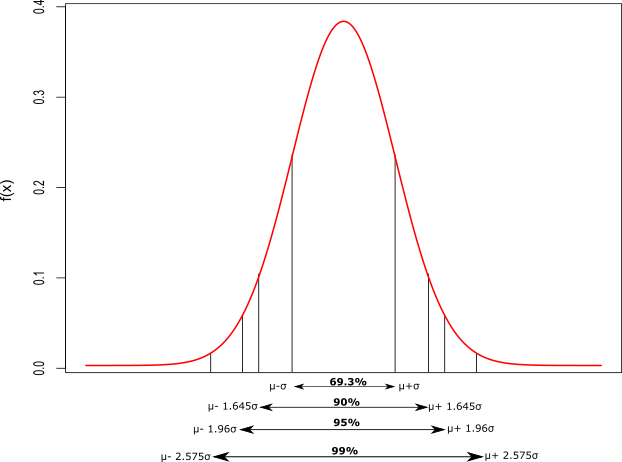
$Distribution de la loi normale avec $\mu$ la moyenne et $\sigma$ l'écart-type$

Figure 8.3: Distribution de la loi normale avec $\mu$ la moyenne et $\sigma$ l’écart-type

Exemple : La longueur des araignées de mer Maja squinado capturées au casier dans la rade de Cherbourg sont en moyenne de 145mm avec un écart-type de 24.3mm. Si l’on admet que la longueur des araignées suit une distribution normale. Quelle est la probabilité de capturer un individu d’une longueur supérieure à 200mm?

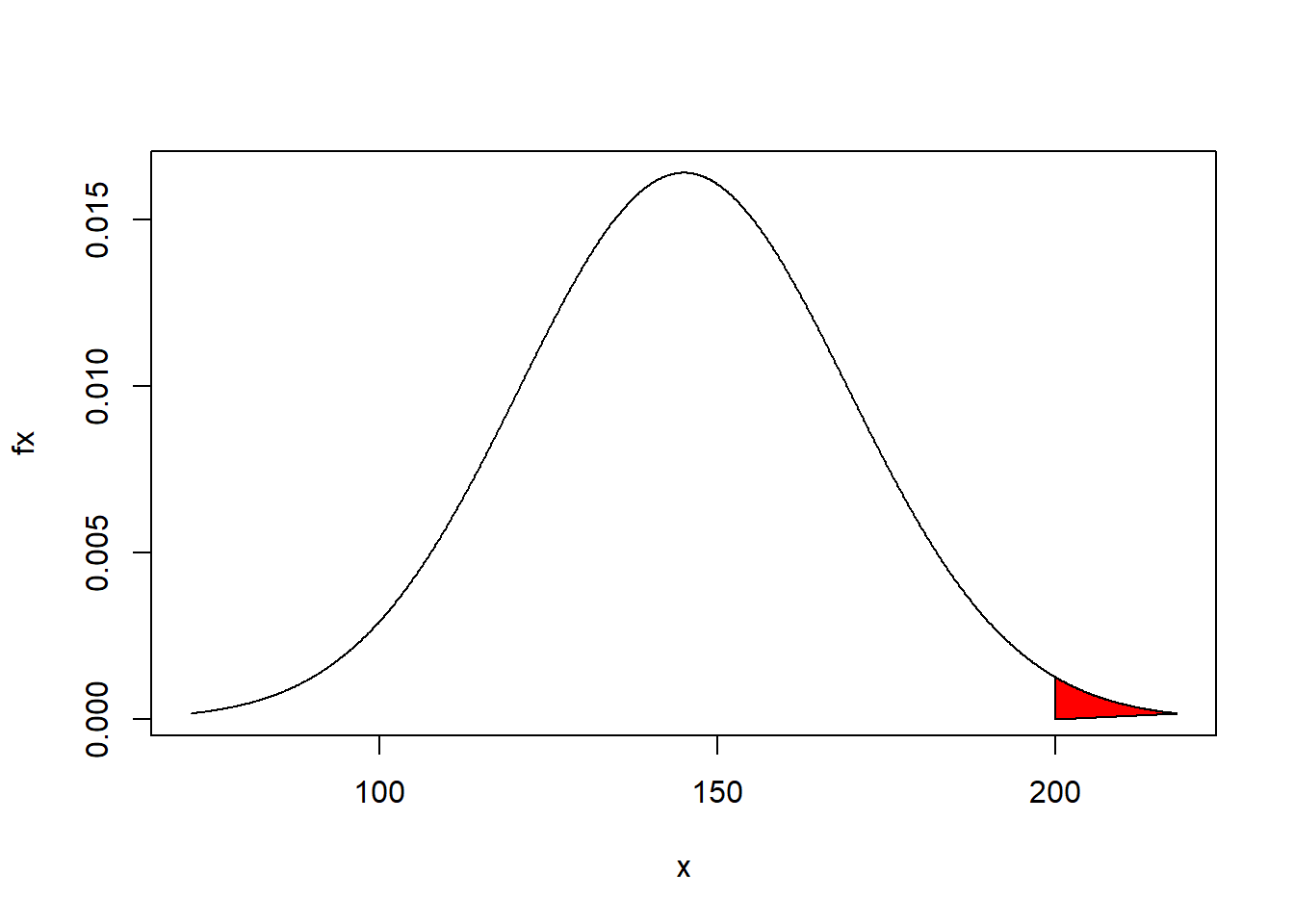
Distribution de la variable aléatoire X 'Longeur des araignées de mer pêchées au casier dans la rade de cherbourg'. La partie rouge correspond à $P(X>200)$

Figure 8.4: Distribution de la variable aléatoire X ‘Longeur des araignées de mer pêchées au casier dans la rade de cherbourg’. La partie rouge correspond à $P(X>200)$

## [1] 0.01180631

8.3.2 La loi Exponentielle

Type de variable : Variables continues

Description : La loi exponentielle correspond souvent à des évènements dont la probabilité de survenir diminue avec le temps. Elle est donc souvent utilisée pour modéliser des durées de vie.

Elle s’écrit $Exp(\lambda)$

avec $\lambda$ : forme de la courbe

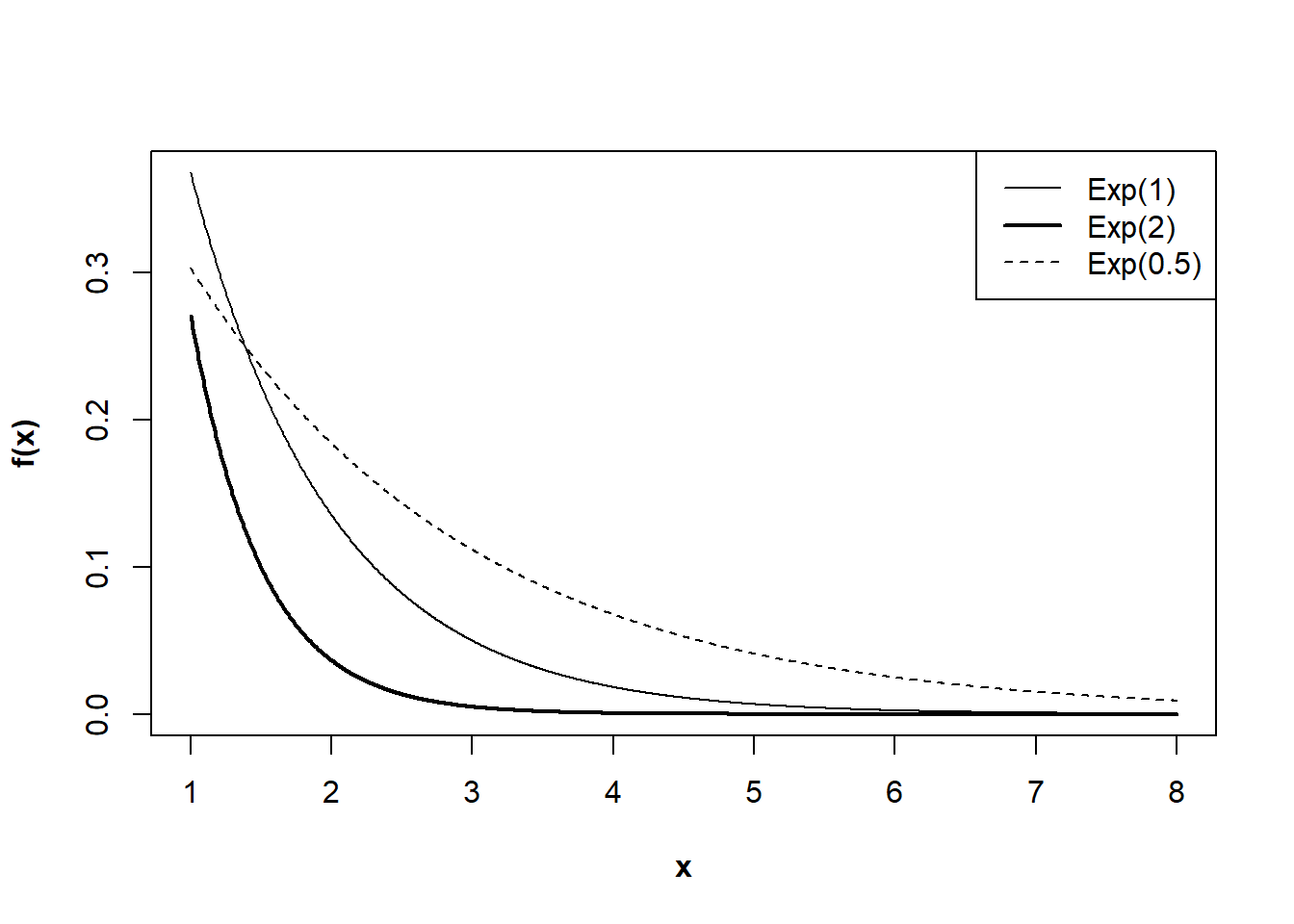
Exemple : Le nombre moyen de départ par jour des anguilles pour la mer des Sargasses est de 1.5 $ind.j^{-1}$. En supposant que le départ des anguilles pour la grande migration est un caractère aléatoire et individuel. Quelle est la probabilité d’attendre plus de 3 jours pour capturer une anguille?

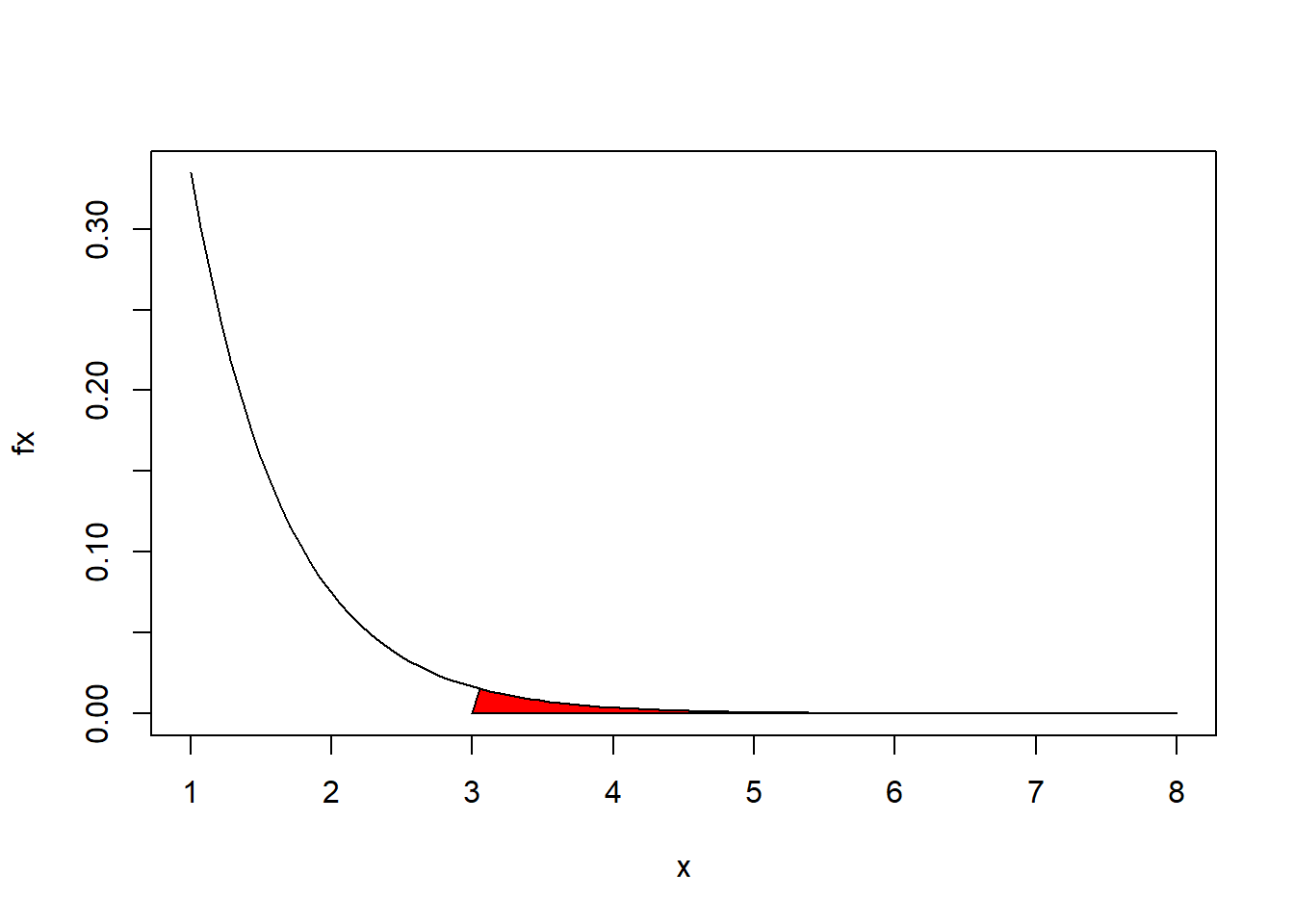
## [1] 0.011109